Cómo ajustar correctamente un PID

Este artículo viene a resumir el fantástico vídeo que Peter Harrison hizo hace unos días en YouTube sobre la manera más sencilla y efectiva de ajustar un PID en escasos minutos en vez de días. He seguido ese vídeo para ajustar el PID de LibreServo y los resultados han sido asombrosos.

En Internet hay cientos de guías de cómo ajustar un PID y todos se pueden resumir en los siguientes sencillos pasos:

• Poner a cero K_D y K_I e incrementar K_P hasta que el sistema corrija el error y empiece a oscilar. Ese sería el máximo de K_P
• Incrementar K_D hasta que la oscilación de K_P se detenga
• Incrementar K_I levemente para que el sistema corrija totalmente el error

Parecen tres pasos sencillos y rápidos, pero la realidad es que al final se convierte en una suerte de intentar adivinar las constantes y tras cientos de pruebas y horas, si tienes suerte, consigues un PID relativamente estable. Es una tarea bastante engorrosa que pocas veces consigue llegar a un resultado totalmente satisfactorio.

Olvidémonos de todo ello e intentemos obtener K_P y K_D de forma matemática. K_I en un sistema dinámico no es necesario en la mayoría de ocasiones e introduce más desventajas que ventajas, así que nos olvidaremos de ella por ahora. A partir de ahora, aunque hable de un PID, realmente me estoy refiriendo a un PD.

Primer paso. Caracterizar tu sistema/motor

Este paso es el más difícil, caracterizar tu sistema. Suponiendo que lo que quieras es manejar un motor, tienes que tener al menos un sistema de lectura del motor, un encóder. No importa que sea súper preciso de 65.000 pasos como en LibreServo o sencillo de 12 pasos como los de Pololu, pero al menos tienes que tener un encóder. Si no tienes un sistema de lectura de tu sistema, entonces no te queda otra que seguir los anteriores tres pasos. Si por el contrario sí dispones de un sensor, un encóder en nuestro caso, entonces continúa.

Vamos a centrarnos en los motores. Para caracterizar un motor tenemos que saber cómo varía su velocidad aplicando un voltaje u otro y cuán rápido cambia la velocidad ante cambios de voltaje. Esta parte la deberemos de hacer con un sistema lo más próximo al final si es que no podemos hacerlo con el verdadero, esto es, si nuestro motor va a ser el motor que mueva un siguelíneas, los resultados serán más cercanos a la realidad si se realizan moviendo el propio siguelíneas o un peso semejante en vez de mover el motor en vacío.

Ganancia del sistema, K_m

Para la primera parte, medimos la velocidad del motor con un PWM del 50%. Para asegurarnos que la velocidad es ya constante, medimos la velocidad transcurridos un tiempo prudencial tras aplicar el PWM, por ejemplo un segundo. Hacer varias medidas y realizar una media. En nuestro caso nos dio 10.205 pasos de encoder cada segundo.

Repetir el mismo procedimiento pero ahora con un PWM del 75%. Realizar varias medidas de la velocidad y hacer la media. En nuestro caso nos dio 15.482 pasos de encóder cada segundo.

Teniendo la velocidad en dos puntos dados, ya podemos obtener la ganancia del sistema. La gancia es lineal, y por lo tanto se ajusta a la fórmula de y = mx + b. Así que sustituyendo obtenemos:
10.205 = m*50 + b
15.482 = m*75 + b
Despejando nos da como resultado: y = 211x - 345. Por tanto, la ganancia del sistema (K_m) es 211.

Constante de tiempo del sistema, T_m

Para la segunda parte, nos interesa no la velocidad que alcanza el motor, sino la rapidez con la que la alcanza. Para ello, con un PWM al 50% del que conocemos la velocidad que alcanza el motor, medimos la rampa de aceleración del motor y vemos en qué momento alcanza el 63% de su velocidad para ese PWM del 50%. En nuestro caso el motor tarda 16ms en alcanzar la velocidad de 6.429, el 63% de 10.205.

No hace falta repetir este segundo paso con un PWM al 75%, ya que debería de darnos el mismo resultado. Aún así, se puede repetir para asegurarnos que estamos en el buen camino.

En la siguiente foto muestro éste mismo proceso que hice para LibreServo donde se ve gráficamente lo comentado:

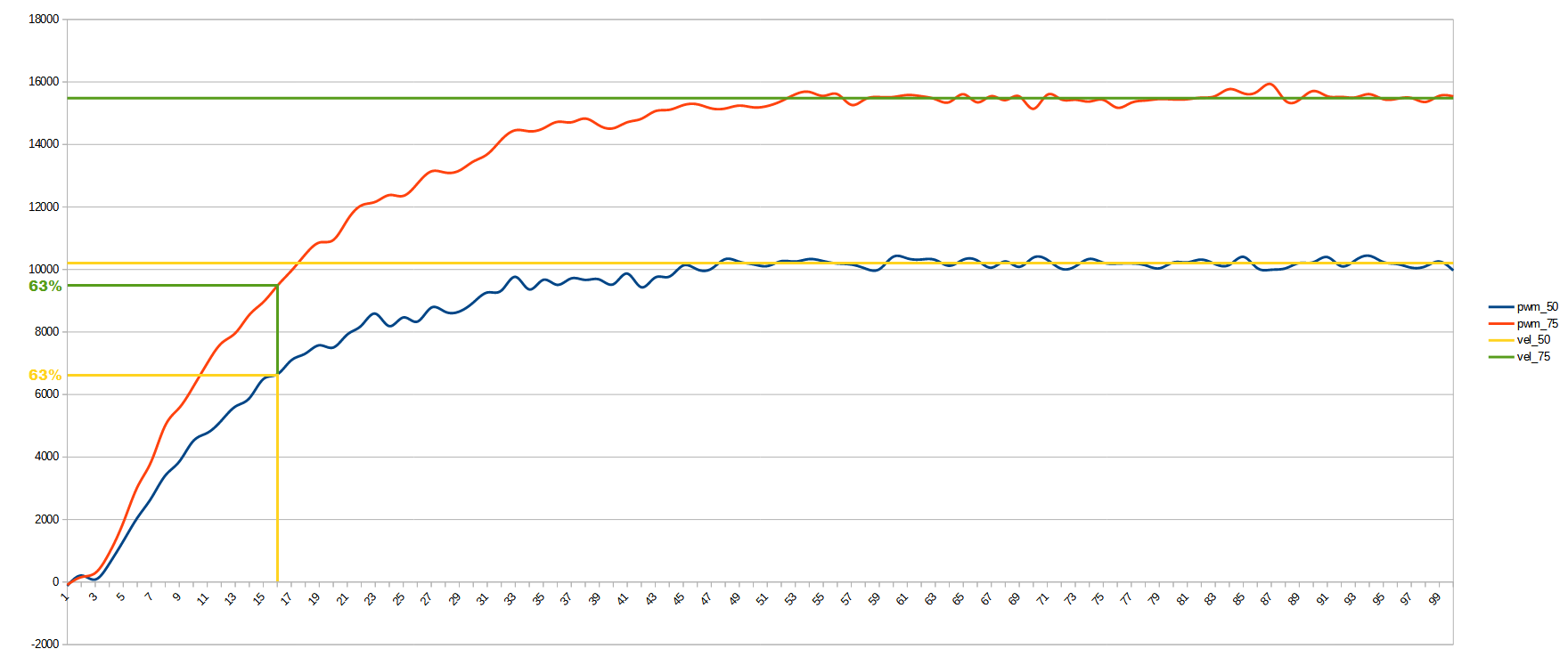Gráfica de la respuesta del motor

Segundo paso. Calcular K_P y K_d

Ya hemos calculado K_m y T_m que son 211 y 0.016 respectivamente en nuestro caso, ahora ya sólo queda la parte sencilla. Pero antes de continuar hay que mencionar a la variable de amortiguación, o ζ.

Variable de amortiguación ζ

Sin entrar en detalles, la variable de amortiguación o ζ (Zeta), afecta a la respuesta de un sistema de segundo orden ante un cambio. Lo que tenemos que saber de esta variable (que utilizaremos luego), es que cualquier valor superior a cero hará al sistema estable antes o después. Uno (1) es el primer valor de ζ en el que no hay rebasamiento en el sistema, valores superiores hacen al sistema más lento. Valores inferiores hacen que llegue al valor destino más rápido pero con rebasamiento. El valor de ζ de 0,707 es el valor más rápido en el que el sistema alcanza el valor destino y no rebasa en más de un 5%. Este valor, 0,707 suele ser el valor elegido para ζ.

En la siguiente imagen cortesía de sumemura.jp, vemos gráficamente lo comentado hasta ahora:

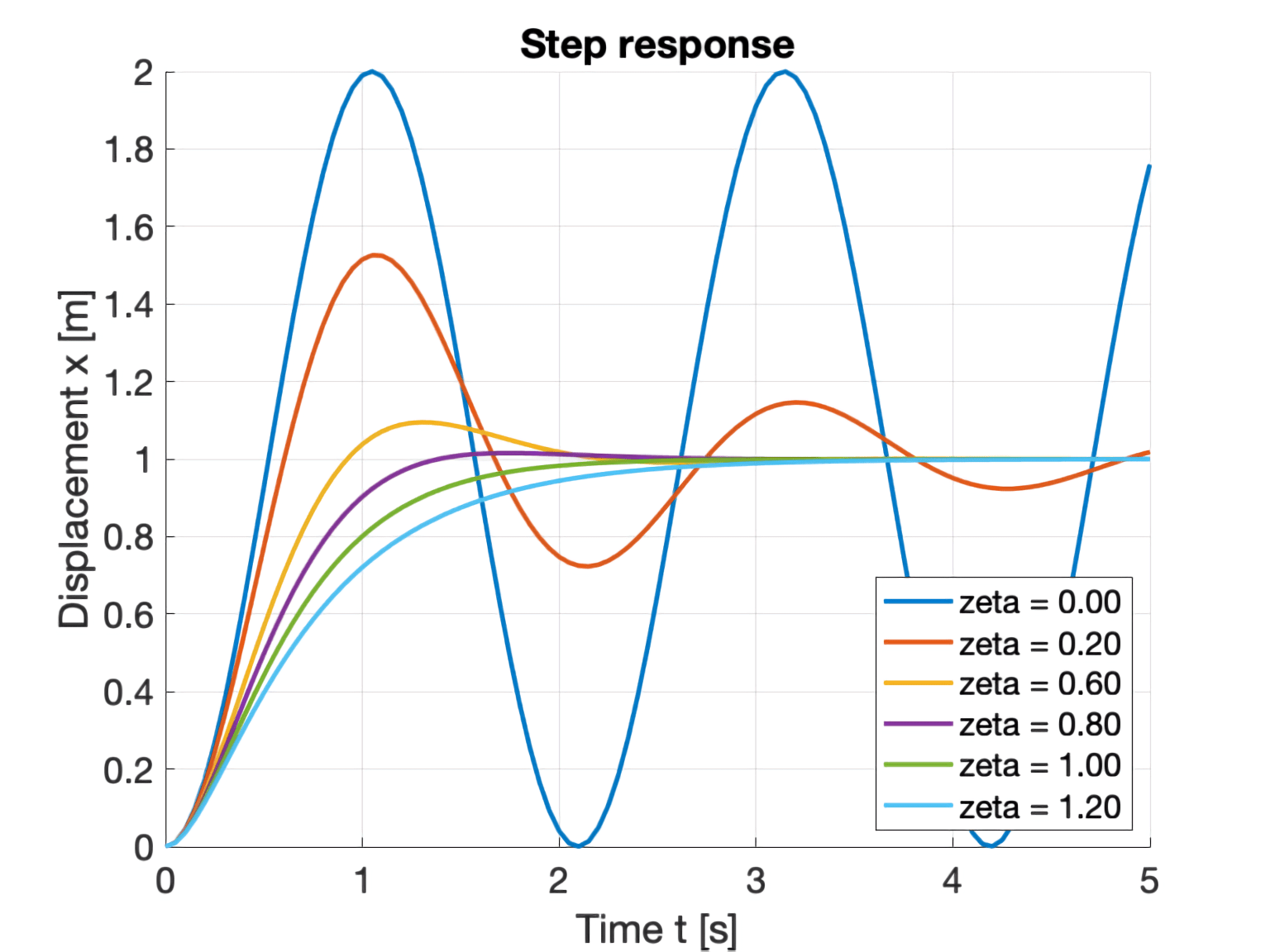Respuesta de un sistema de segundo orden a un cambio

Cálculo de K_P y K_D

Ahora sí, calculemos las variables de K_P y K_D. Para ello haremos uso de las dos siguientes fórmulas:
K_P = T_m⁄K_m · 16⁄ζ²T²_D
K_D = 8T_m-T_D⁄T_DK_m

Pudiera parecer muy complejo, pero tenemos ya todas las variables excepto T_D, tiempo de estabilización. Para ello un buen valor por el que empezar sería el mismo que T_m o la mitad de éste. Si utilizamos la mitad, las fórmulas en nuestro caso quedarían:
K_P = 0,016⁄211 · 16⁄0.707²0,008² = 38
K_D = 8·0,016-0,008⁄0,008·211 = 0,0711
El valor de K_D lo multiplicamos por la frecuencia de nuestro PID, 4KHz, dóndonos un valor de 284. Ese será el valor a sustituir en nuestro código PID.

En la siguiente gráfica se muestra la respuesta del motor de LibreServo con los valores que había conseguido de manera manual, y que notaba que debía seguir optimizando, y la respuesta con los nuevos valores calculados. El motor trata de seguir una curva hermítica, que nos viene perfecto para ver el comportamiento de este a diferentes velocidades:

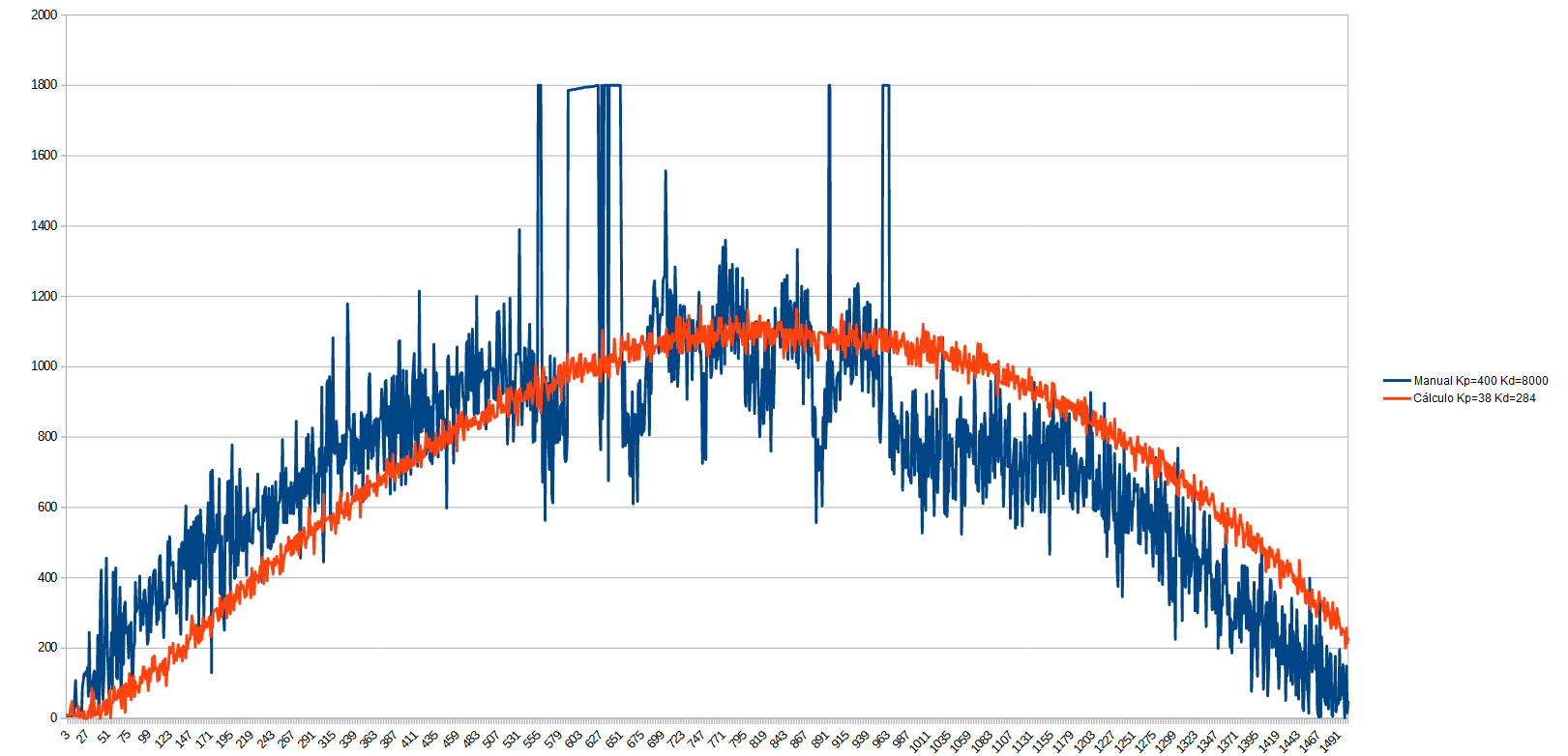Comparativa PWM en motor con diferentes PIDs

Vemos que el PID original saturaba el motor en varias situaciones, y aunque seguía correctamente la curva de movimiento, ese control era muy dañino para la mecánica del motor, en cambio, con los nuevos valores calculados, hemos conseguido a la primera un control casi ideal. Vemos que tiene un cierto retardo en la respusta, así que reduzcamos T_m a 0,004:

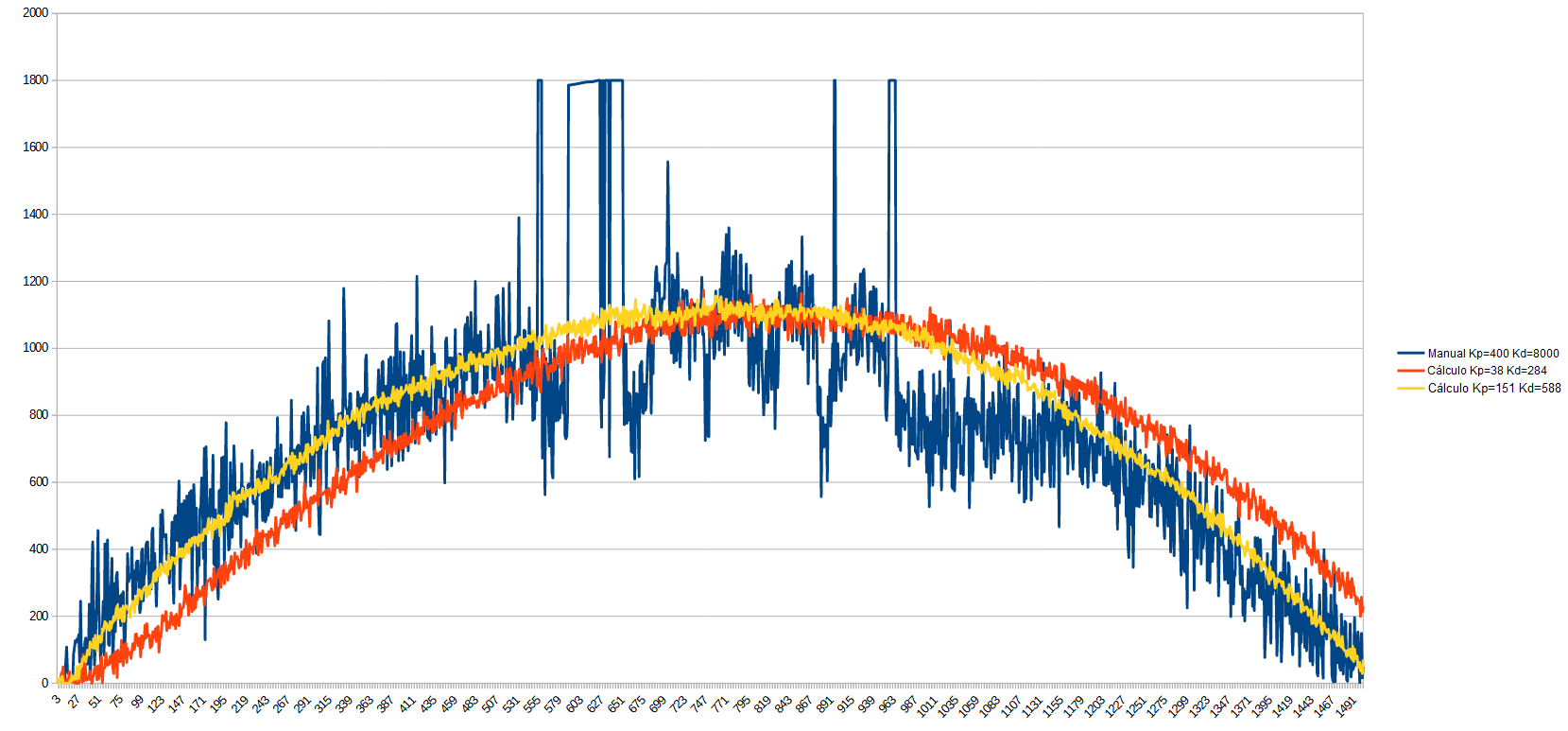Comparativa PWM en motor con diferentes PIDs

¡Ahora ya sí! Hemos conseguido una respuesta practicamente perfecta en tan sólo dos intentos y pocos minutos. Pero, ¿qué pasa si reducimos aún más T_m? Veamos qué pasa cuando T_m lo reducimos aún más, por ejemplo a 0,002:

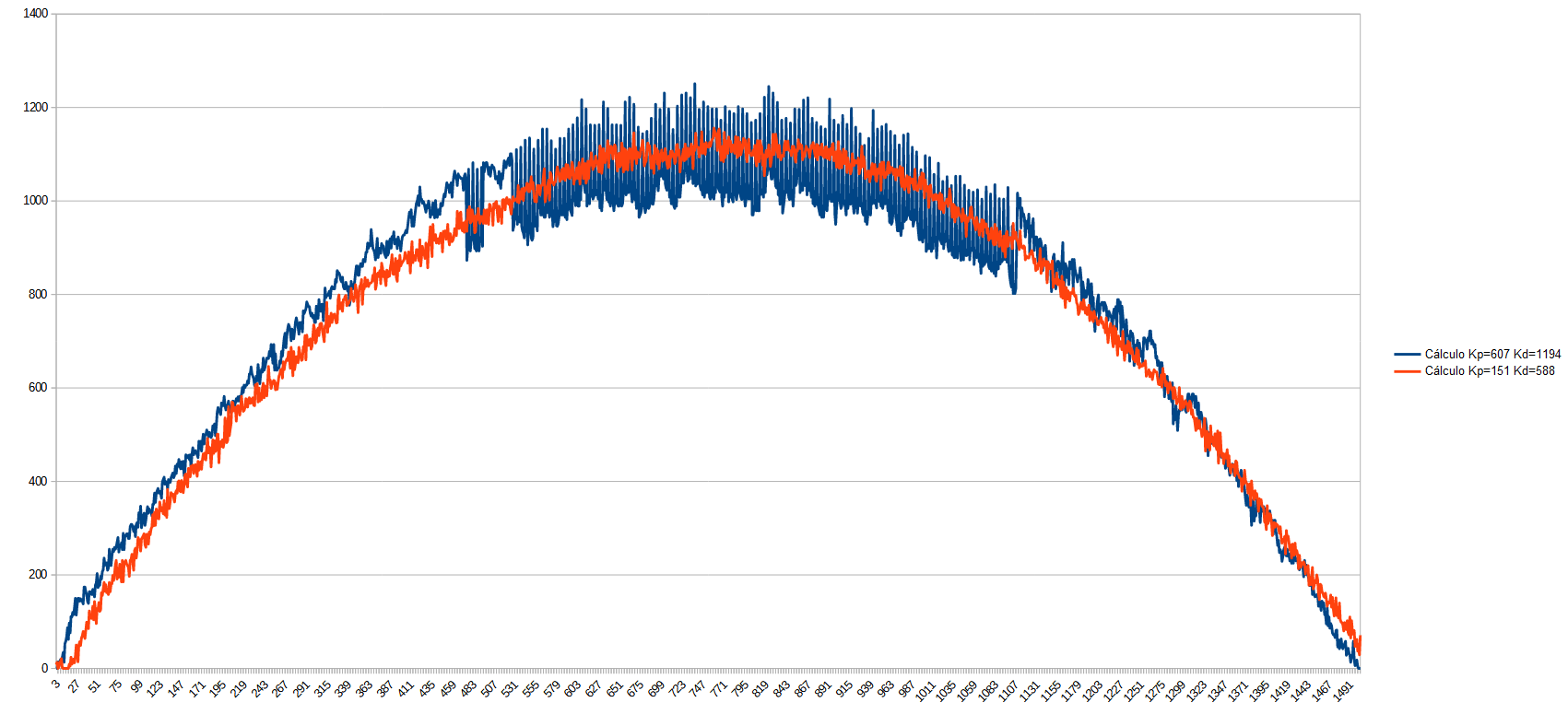Comparativa PWM en motor con diferentes PIDs

Ahora vemos que reducir demasiado T_m provoca que el control ya no sea tan eficaz y empiezan a aparecer ruidos, por lo tanto, nos quedamos con el anterior PID.

En el siguiente vídeo podemos fijarnos en el sonido del servomotor. El movimiento es el mismo, pero con un PID el sonido del motor no se oye correcto y con el segundo PID se oye algo mucho más natural y correcto.

Consideraciones específicas de LibreServo

En el caso de LibreServo, se añade una pequeña distinción entre el PID durante un movimiento y el PID en estático, manteniendo una posición. Durante el movimiento el PID será realmente un PD, pero en estático el PID cambia y se le añade la parte integral, esto se hace así para asegurarnos que en cualquier circunstancia y carga el servomotor mantenga su posición y en muchos casos termine de centrar la posición final.